import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
mtcars = sm.datasets.get_rdataset('mtcars').data1 Introdução
1.1 Regressão linear
Regressão linear é uma ferramenta estatística usada para modelar a relação entre uma variável dependente e uma ou mais variáveis independentes, assumindo que essa relação pode ser descrita por uma linha reta. A ideia de se utilizar é uma é dado a sua simplicidade, tendo apenas um parâmetro de inclinação e um de intercepto, uma outra é que aqui se assume que as variáveis apresentam uma relação linear. A linha representa a melhor aproximação da tendência central dos dados. Aqui devemos partir de uma amostra, um par ordenado \(\{x_{i},y_{i}\}^{N}_{i=1}\), encontrar uma reta que melhor se ajusta a média dos dados, para isso, vamos partir da equação de uma reta. \[ y=\alpha + \beta x \]
Onde a ideia aqui é querer entender qual relação em que a variável \(x\) afeta a variável \(y\), temos então que resolver dois problemas: primeiro é encontrar os parâmetros \(\alpha\) e \(\beta\) que melhor se ajusta, sabendo que nem todo o \(y\) pode ser explicado pelo \(x\), temos que adicionar uma variável à equação que consiga captar essa relação no modelo, essa variável será dada por \(u\).
Podemos reescrever a equação acima como sendo um sistema de equações lineares \[ \begin{aligned} y_{1} &= \alpha + \beta x_{1} + u_{1} \\ y_{2} &= \alpha + \beta x_{2} + u_{2} \\ y_{3} &= \alpha + \beta x_{3} + u_{3} \\ & \vdots \\ y_{n} &= \alpha + \beta x_{n} + u_{n} \end{aligned} \]
Note que esse é um sistema de \(n\) equações lineares com \(n + 2\) incógnitas. E que pela regra de Cramer, sabemos que o sistema apresenta infinitas soluções. O que não nos ajuda e precisamos voltar ao problema, quais valores de \(\alpha\) e \(\beta\) que melhor se ajusta? Uma maneira de se fazer isso, é minimizar a soma do erro quadrático \(\left(\sum_{i=1}^{N} u_i^{2}\right)\) e para isso, vamos isolar o erro, elevar tudo ao quadrado e aplicar a recursividade. \[ \sum_{i=1}^{N} u_i^{2} = \sum_{i=1}^{N} (y_{i} - \alpha - \beta x_{i})^{2} \]
Dado isso, podemos dizer que podemos estimar valores de \(\alpha\) e \(\beta\) que minimizam o erro quadrático. Seja \(S(\alpha, \beta) = \sum_{i=1}^{N} u_i^{2}\) e sabendo que os valores dos parâmetros que zeram o gradiente \(\nabla = \left(\frac{\partial S}{\partial \hat{\alpha}}, \frac{\partial S}{\partial \hat{\beta}}\right)=0\) são os valores que minimizam o erro quadrático. Fazendo as derivadas… \[ \begin{aligned} \nabla = \begin{bmatrix} \dfrac{\partial S}{\partial \hat{\alpha}} \\ \dfrac{\partial S}{\partial \hat{\beta}} \end{bmatrix} = \begin{bmatrix} -2\sum_{i=1}^{N} (y_{i} - \hat{\alpha} - \hat{\beta} x_{i}) \\ -2\sum_{i=1}^{N} (y_{i} - \hat{\alpha} - \hat{\beta} x_{i})(x_{i}) \end{bmatrix} = 0 \end{aligned} \]
Podemos multiplicar ambos os lados por \(-\frac{1}{2}\) e abrir o somatório1. \[ \begin{aligned} \begin{bmatrix} \sum_{i=1}^{N} y_{i} - n\hat{\alpha} - \hat{\beta}\sum_{i=1}^{N} x_{i} \\ \sum_{i=1}^{N} y_{i}x_{i} - \hat{\alpha}\sum_{i=1}^{N}x_{i} - \hat{\beta}\sum_{i=1}^{N} x_{i}^{2} \end{bmatrix} = 0 \end{aligned} \]
Separando os termos, temos que \[ \begin{aligned} \begin{bmatrix} \sum_{i=1}^{N} y_{i} \\ \sum_{i=1}^{N} y_{i}x_{i} \end{bmatrix} = \begin{bmatrix} n\hat{\alpha} + \hat{\beta}\sum_{i=1}^{N} x_{i} \\ \hat{\alpha}\sum_{i=1}^{N}x_{i} + \hat{\beta}\sum_{i=1}^{N} x_{i}^{2} \end{bmatrix} \end{aligned} \] \[ \begin{aligned} \begin{bmatrix} \sum_{i=1}^{N} y_{i} \\ \sum_{i=1}^{N} y_{i}x_{i} \end{bmatrix} = \begin{bmatrix} n & \sum_{i=1}^{N} x_{i} \\ \sum_{i=1}^{N} x_{i} & \sum_{i=1}^{N} x_{i}^{2} \end{bmatrix} \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} \end{aligned} \]
Podemos reorganizar da seguinte maneira: \[ \begin{bmatrix} n & \sum_{i=1}^{N} x_{i} \\ \sum_{i=1}^{N} x_{i} & \sum_{i=1}^{N} x_{i}^{2} \end{bmatrix} \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{N} y_{i} \\ \sum_{i=1}^{N} y_{i}x_{i} \end{bmatrix} \]
Pré-multiplicando ambos os lados pelo inverso da matriz que tem os valores de \(x\): \[ \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} = \begin{bmatrix} n & \sum_{i=1}^{N} x_{i} \\ \sum_{i=1}^{N} x_{i} & \sum_{i=1}^{N} x_{i}^{2} \end{bmatrix}^{-1} \begin{bmatrix} \sum_{i=1}^{N} y_{i} \\ \sum_{i=1}^{N} y_{i}x_{i} \end{bmatrix} \]
Para termos certeza de que este é o ponto mínimo, devemos avaliar a matriz hessiana: \[ H = \begin{bmatrix} \dfrac{\partial^2 S}{\partial \alpha^2} & \dfrac{\partial^2 S}{\partial \alpha \, \partial \beta} \\ \dfrac{\partial^2 S}{\partial \alpha \, \partial \beta} & \dfrac{\partial^2 S}{\partial \beta^2} \end{bmatrix} \]
Logo: \[ H = \begin{bmatrix} n & \sum x_{i} \\ \sum x_{i} & \sum x_{i}^{2} \end{bmatrix} \]
Para ser um mínimo global, devemos ter que:
- O primeiro menor principal será \(> 0\)
- O determinante do segundo menor principal será \(>0\)
Com isso, podemos dizer que é um ponto de mínimo.
Podemos reescrever: \[ \begin{bmatrix} n & \sum x_{i} \\ \sum x_{i} & \sum x_{i}^{2} \end{bmatrix} \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} = \begin{bmatrix} \sum y_{i} \\ \sum x_{i} y_{i} \end{bmatrix} \]
Abrindo: \[ \begin{bmatrix} 1 & 1 & \dots & 1 \\ x_{1} & x_{2} & \dots & x_{n} \end{bmatrix}' \begin{bmatrix} 1 & x_{1} \\ 1 & x_{2} \\ \vdots \\ 1 & x_{n} \end{bmatrix} \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} = \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{bmatrix} \]
Onde: \[ X = \begin{bmatrix} 1 & 1 & \dots & 1 \\ x_{1} & x_{2} & \dots & x_{n} \end{bmatrix}' \] \[ \hat{B} = \begin{bmatrix} \hat{\alpha} \\ \hat{\beta} \end{bmatrix} \] \[ Y = \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{bmatrix} \]
Então: \[ X' \hat{B} = X' Y \] \[ (X' X) \hat{B} = X' Y \] \[ (X' X)^{-1} (X' X) \hat{B} = (X' X)^{-1} X' Y \] \[ \hat{B} = (X' X)^{-1} X' Y \] \[ \boxed{\hat{B} = (X' X)^{-1} X' Y} \]
Então, sempre que estamos falando do estimador do MQO, estamos nos referindo à Equação 1.1: \[ \hat{B} = (X' X)^{-1} X' Y \tag{1.1}\]
Agora, temos que pensar da seguinte maneira: dado que conseguimos construir os estimadores, como podemos criar seus intervalos de confiança? Para isso, podemos substituir \(Y\) por \(XB + U\):2 \[ \hat{B} = (X' X)^{-1} X' (XB + U) \] \[ = (X' X)^{-1} X' XB + (X' X)^{-1} X' U \]
Assumindo que os dados não tenham problema de multicolinearidade perfeita, a matriz \((X' X)^{-1}\) deve existir para que \(I = (X' X)^{-1} X' X\): \[ \hat{B} = B + (X' X)^{-1} X' U \tag{1.2}\]
Observamos na equação Equação 1.2 que a componente do estimador influenciada pelo erro, especificamente \(X' U\), ilustra uma premissa importante do modelo: \(\mathbb{E}(X | U) = 0\). Isso implica que, idealmente, todas as variáveis explicativas deveriam ser exógenas, não apresentando qualquer correlação com o termo de erro. Mas, é importante reconhecer que, na prática, alcançar uma exogeneidade completa é praticamente inviável; assim, é realista esperar que qualquer modelo econômico possa manifestar algum nível, mesmo que mínimo, de endogeneidade.
Subtraind os dois lados da Equação 1.2 por \(-B\) e pós-multiplicando por \((\hat{B} - B)'\): \[ (\hat{B} - B)(\hat{B} - B)' = (X' X)^{-1} X' U[(X' X)^{-1} X' U]' \]
Desenvolvendo a parte esquerda dessa igualdade, temos que: \[ \begin{bmatrix} \hat{B}_{1} - B \\ \hat{B}_{2} - B \end{bmatrix} \begin{bmatrix} \hat{B}_{1} - B & \hat{B}_{2} - B \end{bmatrix}' \]
Multiplicando e aplicando o operador da esperança: \[ \begin{bmatrix} \mathbb{E}[(\hat{B}_{1} - B)^{2}] & \mathbb{E}[(\hat{B}_{1} - B)(\hat{B}_{2} - B)] \\ \mathbb{E}[(\hat{B}_{1} - B)(\hat{B}_{2} - B)] & \mathbb{E}[(\hat{B}_{2} - B)^{2}] \end{bmatrix} \]
Onde a diagonal principal é a variância de \(\hat{B}_{1}\) e o resto é a covariância, então montamos a matriz de variância-covariância: \[ \begin{bmatrix} \text{Var}(\hat{B}_{1}) & \text{Cov}(\hat{B}_{1}, \hat{B}_{2}) \\ \text{Cov}(\hat{B}_{1}, \hat{B}_{2}) & \text{Var}(\hat{B}_{2}) \end{bmatrix} \]
A partir disso, poderíamos montar um intervalo de confiança para os betas se não fosse um pequeno problema… Aqui precisamos do valor de \(\beta\), e que só Deus sabe. Vamos então olhar para o lado direito da igualdade3 \[ =(X' X)^{-1} X' UU' X[(X' X)^{-1}]' \] \[ =(X' X)^{-1} X' UU' X(X' X)^{-1} \]
Abrindo \(UU'\) e aplicando o operador da esperança: \[ UU' = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \begin{bmatrix} u_1 & u_2 & \cdots & u_n \end{bmatrix}' \] \[ = \begin{bmatrix} \mathbb{E}(u_1)^{2} & \mathbb{E}(u_1, u_2) & \cdots & \mathbb{E}(u_1, u_n) \\ \mathbb{E}(u_2, u_1) & \mathbb{E}(u_2)^{2} & \cdots & \mathbb{E}(u_2, u_n) \\ \vdots & \vdots & \ddots & \vdots \\ \mathbb{E}(u_n, u_1) & \mathbb{E}(u_n, u_2) & \cdots & \mathbb{E}(u_n)^{2} \end{bmatrix} \] Vamos ter que na diagonal principal é a variância dos erros e \(\forall \, \mathbb{E}(u_{i}, u_{j})\) em que \(i \neq j\) temos a covariância dos erros. Sob as hipóteses de homoscedasticidade4 e não autocorrelação, vamos ter que:
\[ UU' = \begin{bmatrix} \sigma^{2} & 0 & \cdots & 0 \\ 0 & \sigma^{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma^{2} \end{bmatrix} \]
\[ = \sigma^{2} \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix} \]
\[ = \sigma^{2} I \]
Então continuando, vamos ter que:
\[ (X' X)^{-1} X' \sigma^{2} X(X' X)^{-1} \]
\[ = \sigma^{2} (X' X)^{-1} X' X(X' X)^{-1} \]
\[ = \sigma^{2} (X' X)^{-1} \tag{1.3}\]
Agora sim temos uma matriz de variância-covariância(Equação 1.3), mas percebemos que ao longo do caminho foi necessário fazer algumas hipóteses questionáveis, como a homoscedasticidade e não-autocorrelação. Outro problema dessa matriz de variância-covariância é que nela precisamos da média do erro, mas só Deus sabe o erro… o máximo que podemos fazer é procurar uma estimativa para esse erro, e vamos chamá-lo de resíduo. Para diferenciar, o resíduo é a parte do modelo que não conseguimos explicar e o erro é tudo aquilo que afeta o \(Y\), mas não é o \(X\). Então um estimador para a variancia dos resíduos é: \[ \hat{\sigma}^2 = \frac{SQR}{n-k} = \frac{\sum_{i=1}^{n} u^2}{n-k} \] Onde:
- \(n \rightarrow\) Tamanho da amostra
- \(k \rightarrow\) Numero de coeficientes
Estimando uma regressao no python
Primeiro, vamos começar lendo os dados. Aqui vamos utilizar o dataset mtcars, juntos dos pacotes que serão usados
Vamos agora criar uma função que estime os valores dos \(\hat{\beta}\) e calcula o erro padrão de cada coeficiente, isso é importante pois será usado mais tarde para o calculo das estatisticas \(t\). A Função recebe como um argumento ‘data’ nossa base de dados; y é a variavel dependete e x são nossas variáveis explicativas, note que da maneira que foi construida nossa função y e x deve ser strings.
def ols(data, y, x):
X = data[x].values
Y = data[y].values
# Adiciona uma coluna de "1" para gerar o intercepto
X = np.column_stack((np.ones(X.shape[0]), X))
# Calcula OLS
XtX = np.transpose(X) @ X
XtX_inv = np.linalg.inv(XtX)
XtY = np.transpose(X) @ Y
betas = XtX_inv @ XtY
# Calcula os resíduos
residuals = Y - X @ betas
sqr = np.sum(residuals**2) # Soma dos quadrados dos resíduos
n, k = X.shape
residual_variance = sqr / (n - k) # Variância dos resíduos
# Calcula o erro padrão dos coeficientes
standard_errors = np.sqrt(residual_variance * np.diag(XtX_inv))
return betas, standard_errorstendo nossos valores em mãos, precisamos de uma função que calcule as estatisticas t
def t_stats(betas, standard_errors):
# Calcula os valores-t
t_values = betas / standard_errors
return t_valuesPara organizar tudo e melhorar a visibilidade dos dados, precisamos de uma função que pegue todos esses valores que crie um dataframe
def results_dataframe(data, y, x):
# Calcula betas e erros padrão
betas, standard_errors = ols(data, y, x)
# Calcula estatísticas t
t_values = t_stats(betas, standard_errors)
# Cria um DataFrame para uma melhor visualização
coef_names = ['Intercept'] + x
results = pd.DataFrame({
'Coeficiente': betas,
'Erro Padrão': standard_errors,
'Estatistica t': t_values
}, index=coef_names)
return resultsTemos entao
results_dataframe(mtcars, 'mpg', ['cyl', 'disp'])| Coeficiente | Erro Padrão | Estatistica t | |
|---|---|---|---|
| Intercept | 34.660995 | 2.547004 | 13.608536 |
| cyl | -1.587277 | 0.711844 | -2.229809 |
| disp | -0.020584 | 0.010257 | -2.006696 |
1.2 Conceitos de Convergência
A ideia aqui é entender o que acontece com a amostra à medida que seu tamanho vai para infinito. Embora isso seja puramente teórico, conseguimos tirar algumas ideias para o caso da amostra finita. As duas ideias principais são:
- A lei dos grandes números diz que a média da amostra \(X_n = \frac{1}{n} \sum_{i=1}^n X_i\) converge em probabilidade para a expectativa \(\mu = \mathbb{E}(X_i)\). Isso significa que \(X_n\) está próximo de \(\mu\) com alta probabilidade.
- O teorema do limite central diz que \(\sqrt{n}(X_n - \mu)\) converge em distribuição para uma distribuição Normal. Isso significa que a média da amostra tem aproximadamente uma distribuição Normal para grandes valores de \(n\).
Definição 1.1 (Convergencia) A sequência5 de variáveis aleatórias, \(X_{1}, X_{2}, \ldots\), converge em probabilidade para uma variável aleatória \(X\), se \(\forall \varepsilon > 0\),
\[ \lim_{n \to \infty} \mathbb{P}(\left|X_{n} - X\right| \geq \varepsilon) = 0 \quad \text{ou} \quad \lim_{n \to \infty} \mathbb{P}(\left|X_{n} - X\right| < \varepsilon) = 1 \]
Note que se \(n \to \infty \implies \left|X_{n} - X\right| \to 0\) e isso quer dizer que no limite, a sequência vai se aproximar muito da variável aleatória.
Teorema 1.1 (Teorema da Lei dos Grandes Números - Fraca) Seja \(X_{1}, X_{2}, \ldots\), variáveis aleatórias iid com \(\mathbb{E}[X_{i}] = \mu\) e \(\text{Var}[X_{i}] = \sigma^{2} < \infty\). Defina \(\bar{X}_{n} = \frac{1}{n} \sum_{i=1}^{n} X_{i}\). Então para todo \(\varepsilon > 0\):
\[ \lim_{n \to \infty} \mathbb{P}(|\bar{X}_{n} - \mu| < \varepsilon) = 1 \]
Então, \(\bar{X}_{n}\) converge em probabilidade para \(\mu\).
Mostrar código
def lei_grandes_numeros(pop_mean, pop_std, sample_sizes):
np.random.seed(0) # Para reprodutibilidade
sample_means = [np.random.normal(pop_mean, pop_std, size).mean() for size in sample_sizes]
return np.array(sample_means)
pop_mean = 10
pop_std = 2
n_simulations = 300
sample_sizes = range(1, n_simulations + 1)
# Gerando os dados
sample_means = lei_grandes_numeros(pop_mean, pop_std,sample_sizes)
# Visualização dos resultados
plt.plot(sample_sizes, sample_means, label='Média amostral')
plt.axhline(y=pop_mean, color='r', linestyle='-', label='Média populacional')
plt.xlabel('Tamanho da Amostra')
plt.ylabel('Média')
plt.title('Demonstração da Lei dos Grandes Números')
plt.show()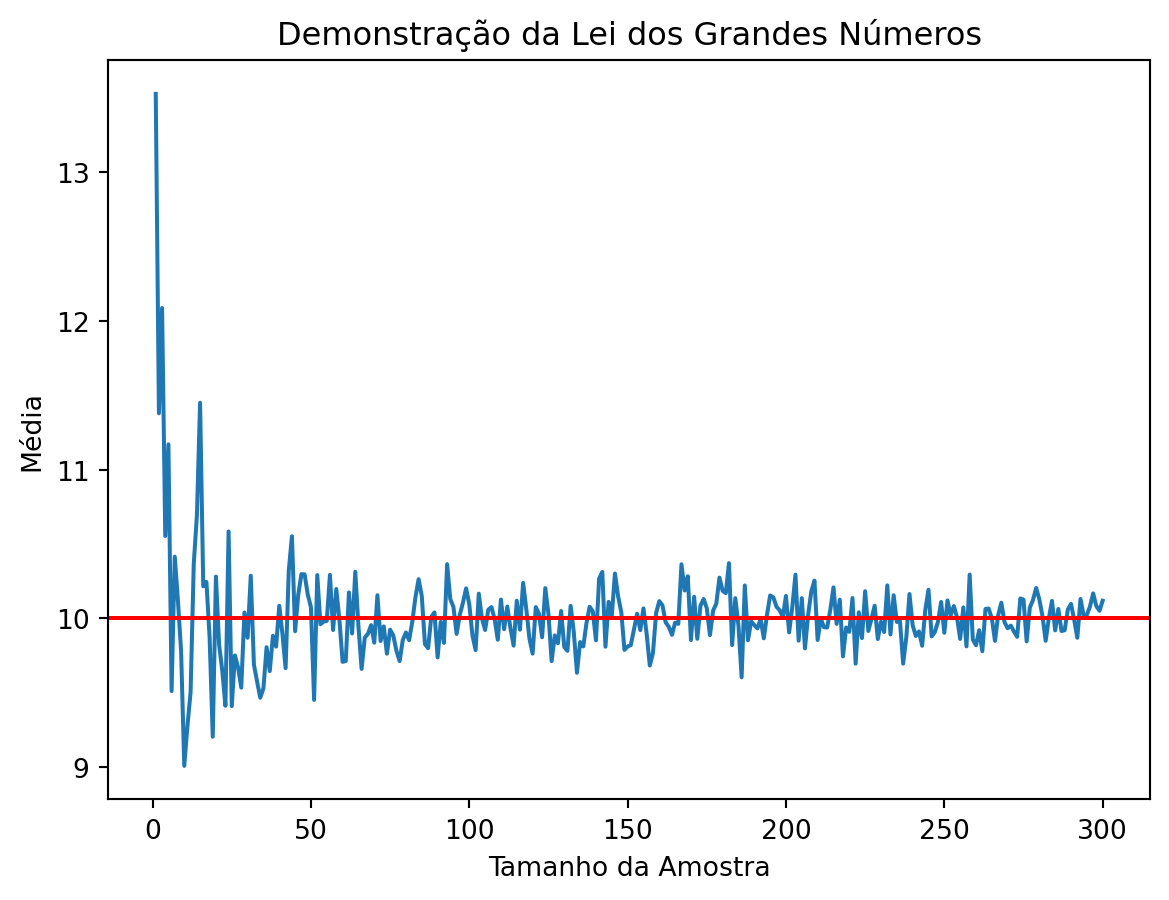
Teorema 1.2 (Teorema do Limite Central) Sejam \(X_{1}, \ldots, X_{n}\) variáveis aleatórias independentes e identicamente distribuídas com média \(\mu\) e variância \(\sigma^2\). Seja \(X_n = \frac{1}{n} \sum_{i=1}^n X_i\). Então,
\[ Z_n = \frac{X_n - \mu}{\sqrt{\frac{\sigma^2}{n}}} = \frac{\sqrt{n}(X_n - \mu)}{\sigma} \xrightarrow[n \to \infty]{} Z \]
onde \(Z\) tem uma distribuição normal padrão. Em outras palavras,
\[ \lim_{n \to \infty} \mathbb{P}(Z_n \leq z) = \Phi(z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2 \pi}} e^{-x^2/2} \, dx. \]
Mostrar código
def tcl(N, pop):
size_sample = 100
sample_mean = [
np.random.choice(pop, size=size_sample, replace=True).mean() for _ in range(N)
]
return np.array(sample_mean)
def plot_tcl(N_values, pop):
fig, axs = plt.subplots(1, len(N_values), figsize=(15, 5), sharey=True)
for i, N in enumerate(N_values):
sample_means = tcl(N, pop)
axs[i].hist(sample_means, bins=30, edgecolor='k', alpha=0.7)
axs[i].set_title(f'{N} Amostras', fontsize=21)
axs[i].set_xlabel('Média da Amostra', fontsize=18)
axs[i].set_ylabel('Frequência', fontsize=18)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
np.random.seed(0)
# Gerar a população
pop = np.random.uniform(size=1000)
# Plota um histograma com diferentes números de amostras
plot_tcl([50, 200, 1000], pop)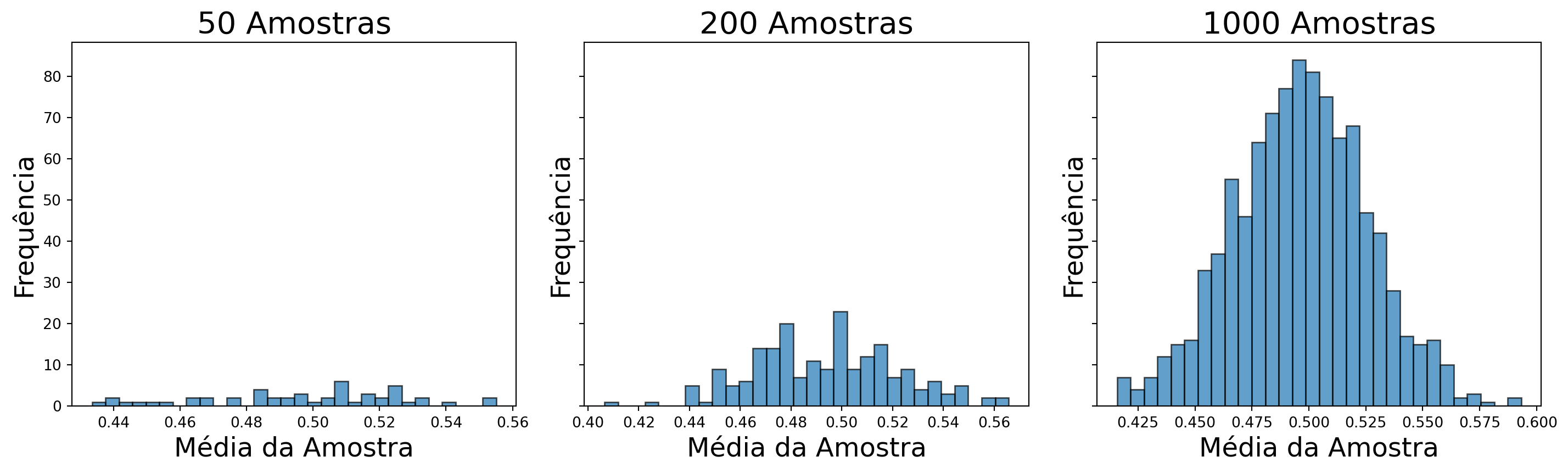
1.3 Séries de tempo
Uma série de tempo é caracterizada por uma sequência de observações tomada sequencialmente no tempo. Podemos chamar essa sequência de observações $ (y_{1},y_{2},y_{3}…) $ como sendo variáveis aleatórias, onde \(y = f(t) + \varepsilon_{t}\), em outras palavras, cada observação é uma função do tempo mais um fator aleatório (ruído branco). Como esse \(y\) depende do tempo, vamos ter um valor diferente de \(y\) para cada valor de \(t=0,1,2,...,T\); \(y^{*} = f(t^{*}) + \varepsilon_{t^{*}}\). Então \(y_{1}\) é o valor de \(y\) no período 1, \(y_{2}\) é o valor de \(y\) no período 2 e assim vai. Uma série de tempo pode ser dividida entre um processo determinístico ou estocástico.
1.3.1 Processo determinístico
É um processo que não depende de um termo aleatório e sempre irá ter o mesmo resultado dado um valor inicial. O processo \(T_{t} = 1 + 0,1t\) é um processo determinístico, pois não depende de nenhum fator aleatório, estando sempre acompanhado de uma constante (1) e um termo de tendência determinística \((0,1t)\).
Podemos observar essa função melhor, gerando o seguinte gráfico no Python.
Mostrar código
def trend(f):
x = np.linspace(0, 100, 1000)
y = f(x)
plt.clf()
plt.plot(x, y)
plt.title(r'$f(x) = 1 + 0.1x$')
plt.show()
# f(x) = 1 + 0.1*x
trend(lambda x: 1 + 0.1 * x)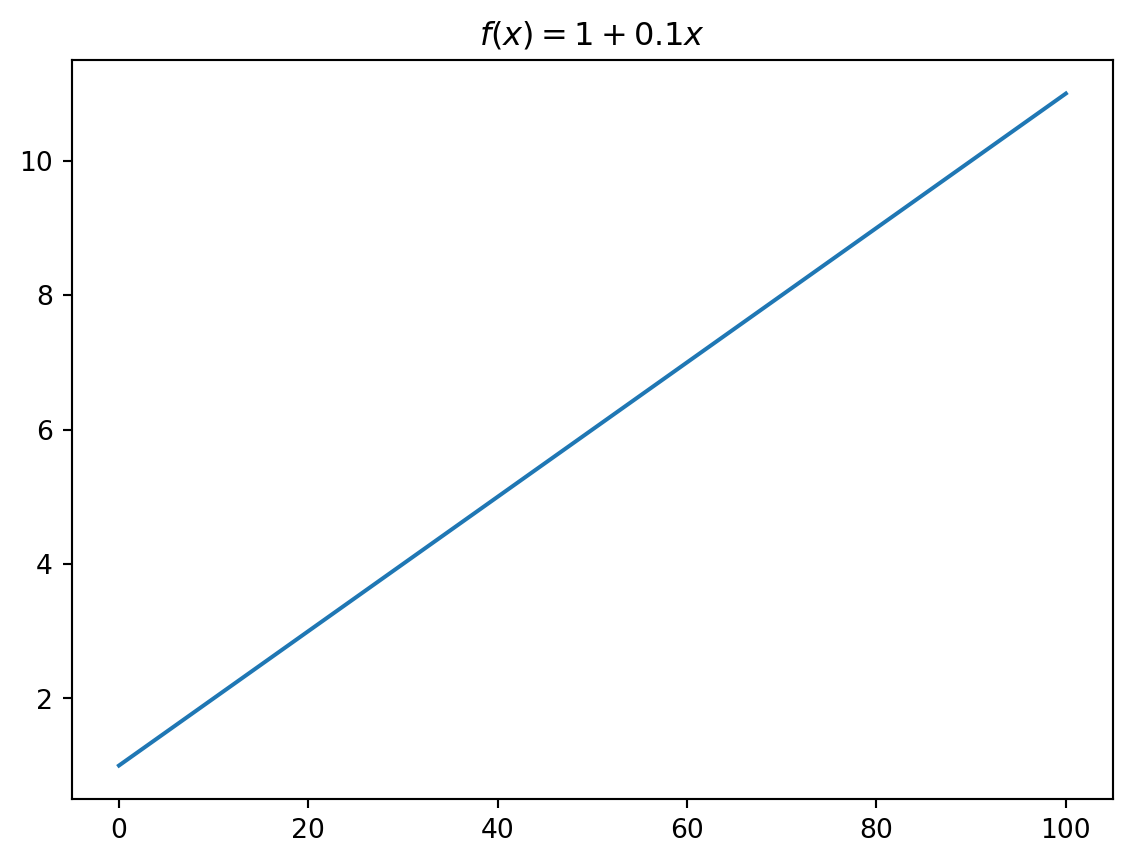
1.3.2 Processo estocástico
O que diferencia um processo estocástico do determinístico é o fator aleatório, por mais que esse fator seja aleatório ele apresenta uma função de distribuição de probabilidade, por mais que se saiba qual é o valor inicial de uma série, não dá para saber com exatidão o próximo valor, mas podemos atribuir probabilidades a diferentes valores.
1.3.2.1 Ruído Branco
Um ruído branco é uma sequência serial de variáveis aleatórias não correlacionadas com média zero e variância finita e constante, seria aquele erro \((u)\) da primeira parte do curso. Assumimos duas condições importantes para o ruído branco: ele deve ser independente um do outro e deve apresentar uma distribuição normal6. Sendo escrito da seguinte forma:
\[ \begin{aligned} \varepsilon_{t} &\sim i.i.d.\mathcal{N}(0, \sigma^2) \\ \varepsilon_{t} &\sim RB(0, \sigma^2) \end{aligned} \]
O ruído branco assume 3 propriedades:
- \(\mathbb{E}[\varepsilon_{t}] = \mathbb{E}[\varepsilon_{t} \mid \varepsilon_{t-1}, \varepsilon_{t-2}, \dotsc] = 0\)
- \(\mathbb{E}[\varepsilon_{t} \varepsilon_{t-j}] = \text{cov}[\varepsilon_{t} \varepsilon_{t-j}] = 0\)
- \(\text{var}[\varepsilon_{t}] = \text{cov}[\varepsilon_{t} \varepsilon_{t}] = \sigma^{2}_{\varepsilon_{t}}\)
As duas primeiras propriedades dizem respeito à impossibilidade de preditividade e à ausência de autocorrelação. A terceira diz respeito à homocedasticidade, a variância ser constante.
Para visualizar isso, criei uma função em Python que gera um conjunto de dados de ruído branco usando a função np.random.normal() que cria um conjunto aleatório de dados de uma distribuição normal, onde \(n\) é o tamanho da amostra desejado.
Mostrar código
def white_noise(n):
np.random.seed(0)
white_noise = np.random.normal(0, 1, n)
plt.clf()
plt.plot(white_noise)
plt.axhline(0, color = 'black')
plt.show()
white_noise(100)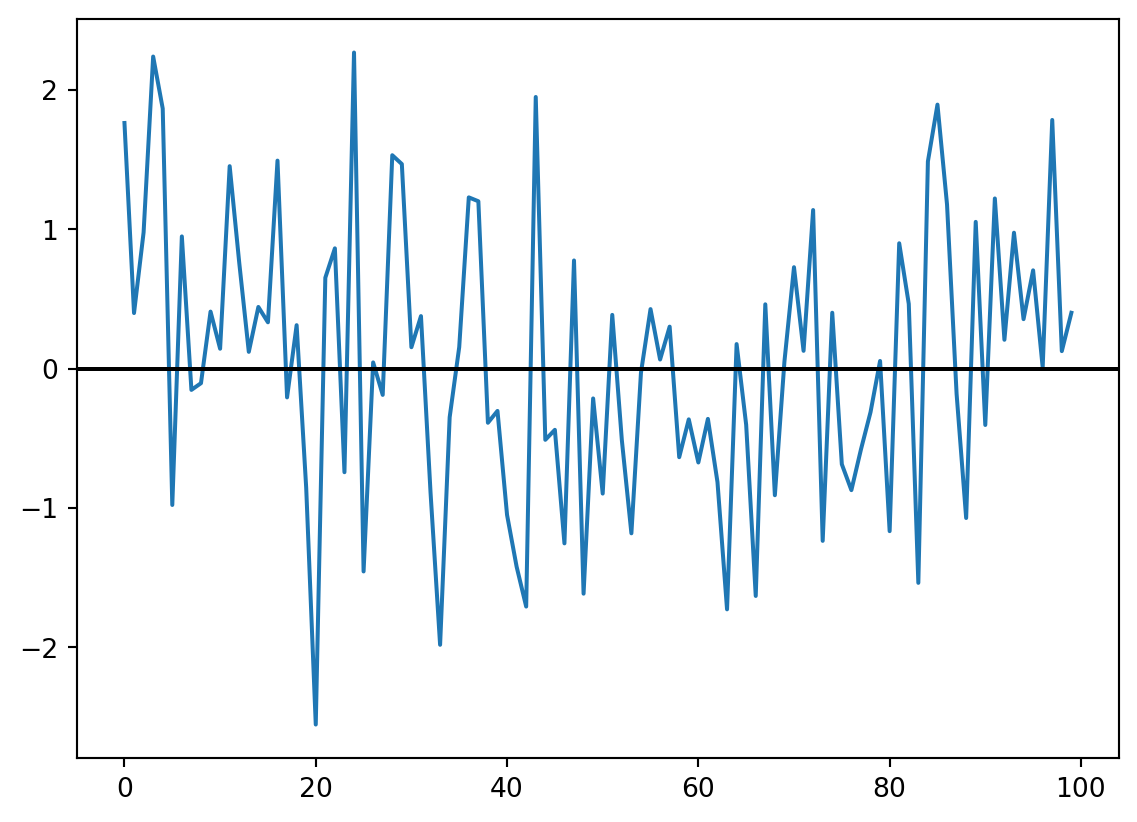
1.3.2.2 Passeio aleatório
Esse tempo passeio aleatório se diz pelo fato de que o valor de uma variável em um determinado período é igual ao seu valor no período passado mais um fator aleatório determinado por \(\varepsilon_{t}\), sendo descrito por:
\[ y_{t} = y_{t-1} + \varepsilon_{t} \]
Vamos supor um valor inicial para \(y_{t}\) como sendo \(y_{1}\), então:
\[ \begin{aligned} y_{1} &= y_{0} + \varepsilon_{1} \\ y_{2} &= y_{1} + \varepsilon_{2} \\ y_{2} &= y_{0} + \varepsilon_{1} + \varepsilon_{2} \end{aligned} \]
Resolvendo isso recursivamente, temos:
\[ y_{t} = y_{0} + \sum_{i=1}^{t} \varepsilon_{i} \]
Se \(y_{0} \sim 0\), podemos então dizer que o passeio aleatório é uma soma acumulada de ruídos brancos:
\[ y_{t} = \sum_{i=1}^{t} \varepsilon_{i} \]
Pode acontecer o caso do passeio aleatório ter uma constante \(\gamma\) adicionada:
\[ y_{1} = \gamma + y_{0} + \varepsilon_{1} \]
Logo, quando \(y_{0} \sim 0\), vamos ter que:
\[ y_{t} = \gamma t + \sum_{i=1}^{t} \varepsilon_{i} \]
Mostrar código
def random_walk(trend, n):
np.random.seed(0)
yt = np.zeros(n)
epsilon = np.random.normal(0,1,n)
for t in np.arange(1,n):
yt[t] = t * trend + np.sum(epsilon[:t+1])
return yt
def plot_rw(trend_list, t):
plt.clf()
for trend in trend_list:
rw = random_walk(trend, t)
plt.plot(rw, label=f'Tendencia = {trend}')
plt.legend()
plt.show()
trend_list = [0, 0.2, -0.2]
plot_rw(trend_list, t=100)
1.3.3 Estacionariedade e Autocorrelação
Antes de entrar no assunto de autocorrelação, devemos ter em mente algumas propriedades referentes ao primeiro momento (esperança) e segundo momento (variância) de um passeio aleatório. O primeiro momento de um passeio aleatório pode ser calculado pela sua média:
\[ \mathbb{E}[y_{t}] = \mathbb{E}[y_{0} + \sum_{i=1}^{t} \varepsilon_{i}] = \mathbb{E}[y_{0}] + \mathbb{E}[\sum_{i=1}^{t} \varepsilon_{i}] = \mathbb{E}[y_{0}] + 0 = y_{0} = \mu \]
Nota-se que a esperança (média) de \(y_{t}\) não depende de \(t\), sendo uma constante e é por isso que estou chamando de \(\mu\).
O segundo momento é a variância:
\[ \text{Var}[y_{t}] = \mathbb{E}[y_{t}^{2}] = \mathbb{E}[(y_{t} - \mathbb{E}[y_{t}])^{2}] \] \[ = \mathbb{E}[y_{t}^{2}] - \mathbb{E}[y_{0}]^{2} \] \[ = \mathbb{E}[(y_{0} + \sum \varepsilon_{i})^{2}] \] \[ = \mathbb{E}[y_{0}^{2} + 2y_{0}\sum \varepsilon_{i} + \sum \varepsilon_{i}^{2}] - \mu^{2} \] \[ = \mathbb{E}[y_{0}^{2}] + 2y_{0}\sum \mathbb{E}[\varepsilon_{i}] + \sum \mathbb{E}[\varepsilon_{i}^{2}] - \mu^{2} \] \[ = \mu^{2} + 0 + \sum \sigma^{2} - \mu^{2} = t \sigma^{2} \]
Podemos observar que a variância de um processo aleatório não é constante, pois vai depender de \(t\).
Outra parada importante é definir a covariância para \(k\) lags:
\[ \text{Cov}[y_{t},y_{t-k}] = \mathbb{E} \{ (y_{t} - \mathbb{E}[y_{t}])(y_{t-k} - \mathbb{E}[y_{t-k}]) \} = \mathbb{E} [(y_{t} - \mu)(y_{t-k} - \mu )] \]
1.3.4 Estacionariedade
A hipótese da estacionariedade é um caso particular do processo estocástico, no qual se assume que o processo está em um estado de equilíbrio. O caso dos processos estritamente estacionários (estacionariedade forte) é quando todas as suas propriedades (momentos) não são afetadas pelo tempo. Como essas condições são muito restritas, na grande maioria das vezes nos referimos a esse processo estocástico como fracamente estacionário, ou covariância-estacionário, ou estacionário de segunda ordem. Isso quer dizer que apenas a média e a variância devem ser constantes e que a covariância deve depender apenas do número de lags \((k)\):
\[ \mathbb{E}[y_{t}] = \mu \] \[ \text{Var}[y_{t}] = \mathbb{E}[(y_{t} - \mu)^{2}] = \sigma^2 \] \[ \text{Cov}[y_{t},y_{t+k}] = \mathbb{E} [ (y_{t} - \mu)(y_{t-k} - \mu)] = \gamma_{k} \]
1.3.5 Função de autocorrelação (FAC)
Ao assumir a hipótese da estacionariedade, vamos ter que a função conjunta de probabilidade de \(y_{t_{1}}\) e \(y_{t_{2}}\) será a mesma para todo o tempo \(t_{1}\) e \(t_{2}\), que será constante. Isso implica que a covariância entre \(y_{t}\) e \(y_{t+k}\) será separada apenas por \(k\) intervalos de tempo (lag). Assim, a autocovariância ao lag \(k\) é definida por:
\[ \gamma_{k} = \text{Cov}[y_{t},y_{t+k}] = \mathbb{E} [ (y_{t} - \mu)(y_{t-k} - \mu)] \]
Da mesma forma, teremos que a autocorrelação é dada por:
\[ \rho_{k} = \dfrac{\mathbb{E} [ (y_{t} - \mu)(y_{t-k} - \mu)]}{\sqrt{\mathbb{E}[(y_{t} - \mu)^{2}] \mathbb{E}[(y_{t} - \mu)^{2}] }} = \dfrac{\mathbb{E} [ (y_{t} - \mu)(y_{t-k} - \mu)]}{\sigma^{2}} \]
Como em um processo estacionário a variância é constante, vamos ter que \(\gamma_{0} = \sigma^{2}\). Podemos então dizer que a autocorrelação no lag \(k\) é:
\[ \rho_{k} = \dfrac{\gamma_{k}}{\gamma_{0}} \]
E isso implica que \(\rho_{0} = 1\) se \(k=0\).
A Função de autocorrelação é quando se plota um gráfico \(\rho_{k}\) contra o lag \(k\).
Note que se somarmos n vezes um parâmetro é o mesmo que dizer n vezes o parâmetro, logo \(\sum_{i=1}^{N}\hat{\alpha} = n\hat{\alpha}\).↩︎
Vale lembrar que \(B\) sem chapéu é o melhor ajuste possível da reta, os valores que só Deus sabe.↩︎
Vale lembrar que \((AB)' = B' A'\)↩︎
Variância dos erros é constante, isto é, \(\mathbb{E}(u_i^2) = \sigma^2, \, \forall i=1, \ldots, n\)↩︎
Lembre-se da ideia de convergência de uma sequência. Dado um \(\varepsilon > 0\), dizemos que \(x_{k} \to x\) se existir um \(k_0\), em que \(\forall k \geq k_0 \implies |x_{k} - x| < \varepsilon\)↩︎
Chamada também de Distribuição normal gaussiana.↩︎